[译] 文生图(text-to-image)简史:扩散模型(diffusion models)的崛起与发展(2022)
译者序
本文翻译自 2022 年的一篇英文博客: The recent rise of diffusion-based models, 另外也参考其他资料补充了一点内容,主要方便自己粗浅理解。
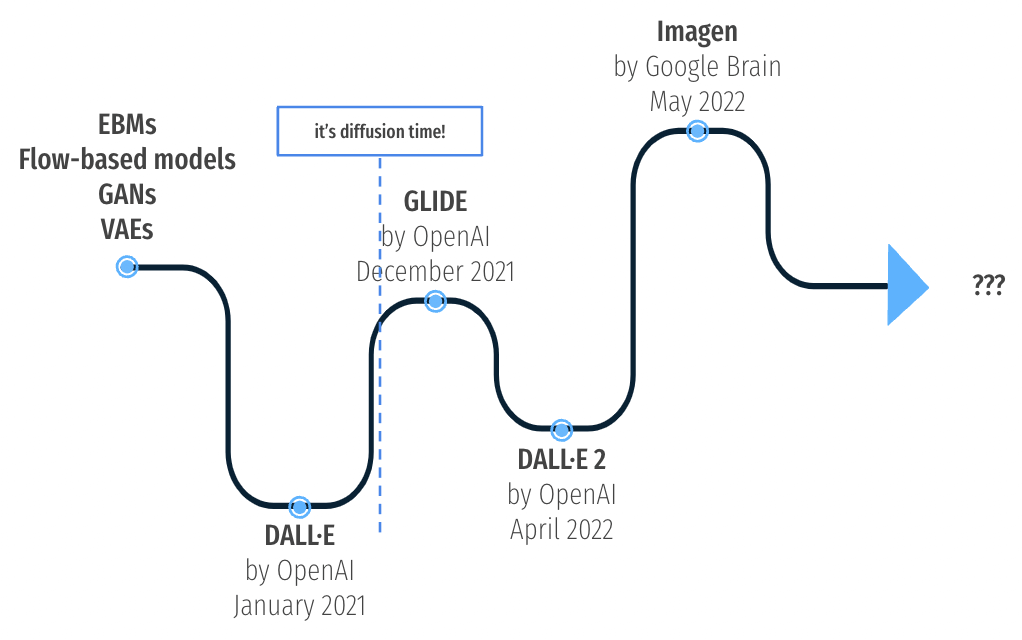
Fig. 文生图(text-to-image)近几年演进
由于译者水平有限,本文不免存在错误之处。如有疑问,请查阅原文。
- 译者序
- 1 OpenAI
DALL·E:起于文本,潜入图像,2021.01 - 2
Diffusion:高斯去噪,扩散称王,2021.12 - 3
GLIDE:文本引导,定向扩散,2022.04 - 4
DALL·E 2:取长补短,先验称奇,2022.04 - 5 Google
Imagen:删繁就简,扩散三连,2022.05 - 6 总结
- 参考资料

Sources: OpenAI DALL·E 2
生成式建模(generative modeling)近几年发展神速, 网上也涌现出了大批令人惊叹的纯 AI 生成图片。 本文试图总结文生图(text-to-image)领域近几年的发展, 尤其是各种扩散模型(diffusion models)—— 它们已经是业界的标杆架构。
1 OpenAI DALL·E:起于文本,潜入图像,2021.01
1.1 GPT-3 (2020):基于 transformer 架构的多模态大语言模型
2020 年,OpenAI 发布了 GPT-3 模型 [1],这是一个基于 Transformer
架构的多模态大语言模型,能够完成机器翻译、文本生成、语义分析等任务,
也迅速被视为最先进的语言建模方案(language modeling solutions)。
1.2 DALL·E (2021.01):transformer 架构扩展到计算机视觉领域
DALL·E [7] 可以看作是将 Transformer(语言领域)的能力自然扩展到计算机视觉领域。
如何根据提示文本生成图片?DALL·E 提出了一种两阶段算法:
-
训练一个离散 VAE (Variational AutoEncoder) 模型,将图像(images)压缩成 image tokens。
VAE 是一种神经网络架构,属于 probabilistic graphical models and variational Bayesian methods 家族。
-
将编码之后的文本片段(encoded text snippet)与 image tokens 拼在一起(
concatenate), 训练一个自回归 Transformer,学习文本和图像之间的联合分布。
最终是在从网上获取的 250 million 个文本-图像对(text-image pairs)上进行训练的。
1.3 量化“文本-图像”匹配程度:CLIP 模型
训练得到模型之后,就能通过推理生成图像。但如何评估生成图像的好坏呢?
OpenAI 提出了一种名为 CLIP 的 image and text linking 方案 [9],
它能量化文本片段(text snippet)与其图像表示(image representation)的匹配程度。
抛开所有技术细节,训练这类模型的思路很简单:
- 将文本片段进行编码,得到 \(\mathbf{T}_{i}\);
- 将图像进行编码,得到 \(\mathbf{I}_{i}\);
对 400 million 个 (image, text) 进行这样的操作,
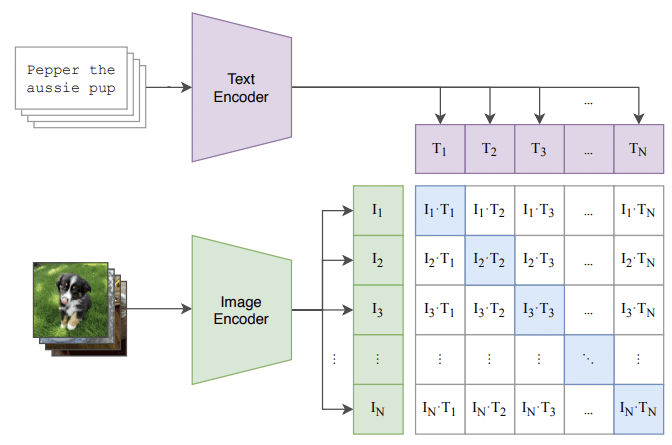
F.g CLIP contrastive pre-training 工作原理 [9]. (文本大意:澳大利亚小狗)。
基于这种映射方式,就能够评估生成的图像符合文本输入的程度。
1.4 小结
DALL·E 在 AI 和其他领域都引发了广泛的关注和讨论。 不过热度还没持续太久,风头就被另一个方向抢走了。
2 Diffusion:高斯去噪,扩散称王,2021.12
Sohl-Dickstein 等提出了一种图像生成的新思想 —— 扩散模型(diffusion models) [2]。 套用 AI 领域的熟悉句式,就是
All you need is
diffusion.
2.1 几种图像生成模型:GAN/VAE/Flow-based/Diffusion
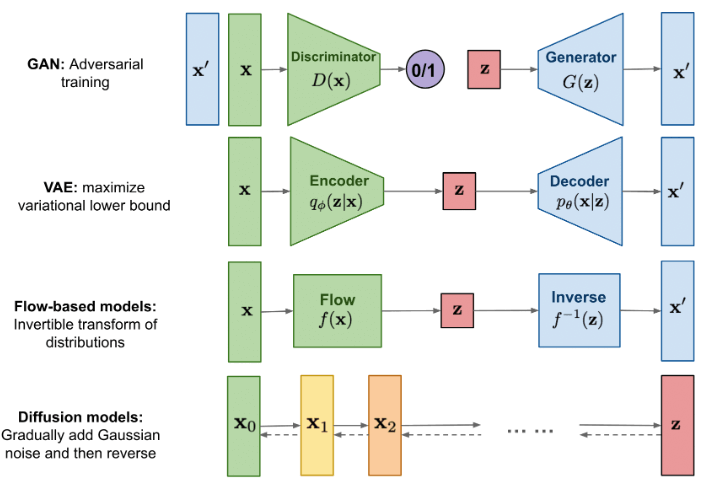
Fig. 几种生成式模型(generative models)[13]
Diffusion 模型受到了非平衡热力学(non-equilibrium thermodynamics)的启发,但其背后是一些有趣的数学概念。 它仍然有大家已经熟悉的 encoder-decoder 结构,但底层思想与传统的 VAE(variational autoencoders)已经不同。
要理解这个模型,需要从原理和数学上描述正向和反向扩散过程。
公式看不懂可忽略,仅靠本文这点篇幅也是不可能推导清楚的。感兴趣可移步 [13-15]。
2.2 正向图像扩散(forward image diffusion)
2.2.1 基本原理
向图像逐渐添加高斯噪声,直到图像完全无法识别。
这个过程可以被形式化为顺序扩散马尔可夫链(Markov chain of sequential diffusion steps)。
2.2.2 数学描述
- 假设图像服从某种初始分布 \(q(\mathbf{x}_{0})\),
- 那么,我们可以对这个分布采样,得到一个图像 \(\mathbf{x}_{0}\),
- 接下来,我们希望执行一系列的扩散步骤,\(\mathbf{x}_{0} \to \mathbf{x}_{1} \to ... \to \mathbf{x}_{T}\),每次扩散都使图像越来越模糊。
- 如何添加噪声?由一个
noising schedule(加噪计划/调度) \(\{\beta_{t}\}^{T}_{t=1}\) 定义, 对于每个 \(t = 1,...,T\),有 \(\beta_{t} \in (0,1)\)。
基于以上定义,我们就可以将正向扩散过程描述为
\[q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)=\mathcal{N}\left(\sqrt{1-\beta_{t}} \mathbf{x}_{t-1}, \beta_{t} \mathbf{I}\right).\]注,
- \(\mathcal{N}\) 可能来自 next 首字母,表示下一个状态的概率分布(马尔科夫状态转移概率);
几点解释:
- 随着加噪次数的增多 \((T \to \infty)\),最终分布 \(q(\mathbf{x}_{T})\) 将趋近于常见的各向同性高斯分布(isotropic Gaussian distribution),这使得未来的采样非常简单和高效。
-
使用高斯核加噪还有一个好处 —— 可以绕过中间加噪步骤,直接得到任意中间状态(intermediate latent state), 这要归功于 reparametrization。直接采样,
\[q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right) = \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \cdot \epsilon,\]其中 \(\alpha_{t} := 1-\beta_{t}\),\(\bar{\alpha}_{t} := \prod_{k=0}^{t}\alpha_{k}\),\(\epsilon \sim \mathcal{N}(0, \mathbf{I})\)。 这里的 \(\epsilon\) 表示高斯噪声 —— 这个公式对于模型训练至关重要。
2.3 反向图像扩散(reverse image diffusion)
2.3.1 基本原理
正向过程定义好了,是否能定义一个反向过程 \(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\), 从噪声回溯到图像呢?
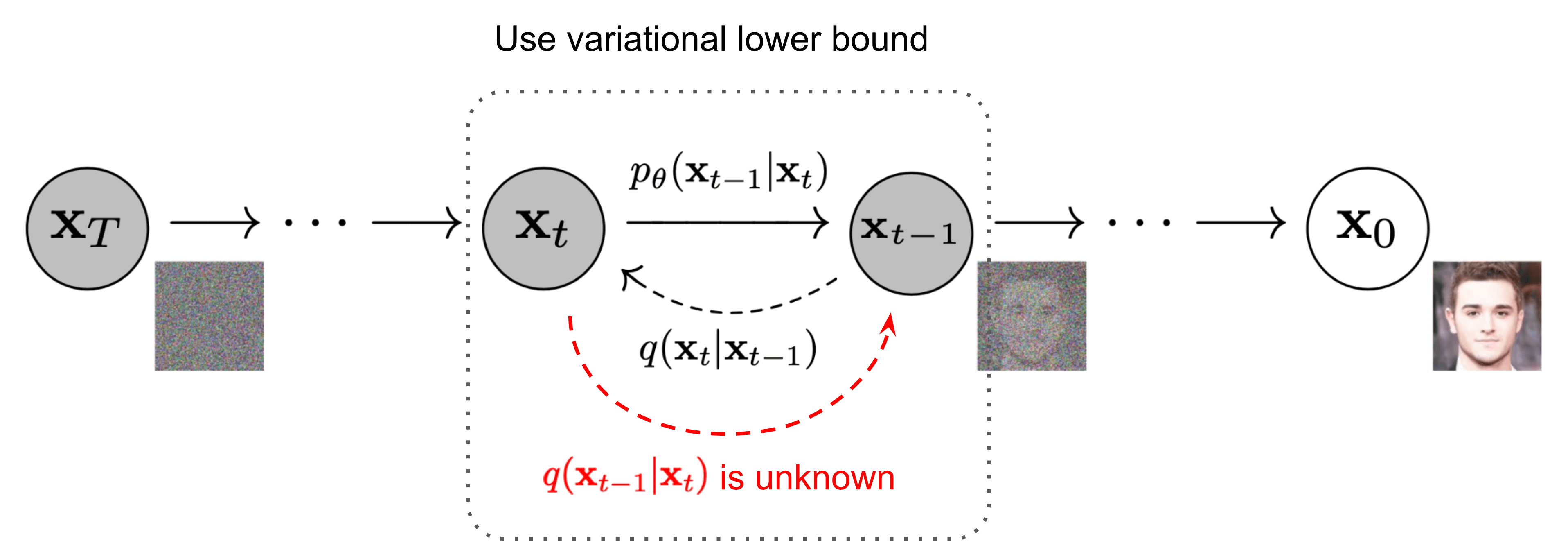
Fig. The Markov chain of forward (reverse) diffusion process of generating a sample by slowly adding (removing) noise [13]
首先,从概念上来说,是不行的;
其次,这需要 marginalization over the entire data distribution。 要从加噪样本返回到起始分布 \(q(\bf{x}_{0})\),必须对所有可能从噪声中得到 \(\mathbf{x}_{0}\) 的方式进行 marginalization,包括所有中间状态。 这意味着计算积分 \(\int q(\mathbf{x}_{0:T})d\mathbf{x}_{1:T}\),这是不可行的。
不过,虽然无法精确计算,但可以近似!
核心思想是以可学习网络(learnable network)的形式,
近似反向扩散过程。
2.3.2 数学表示
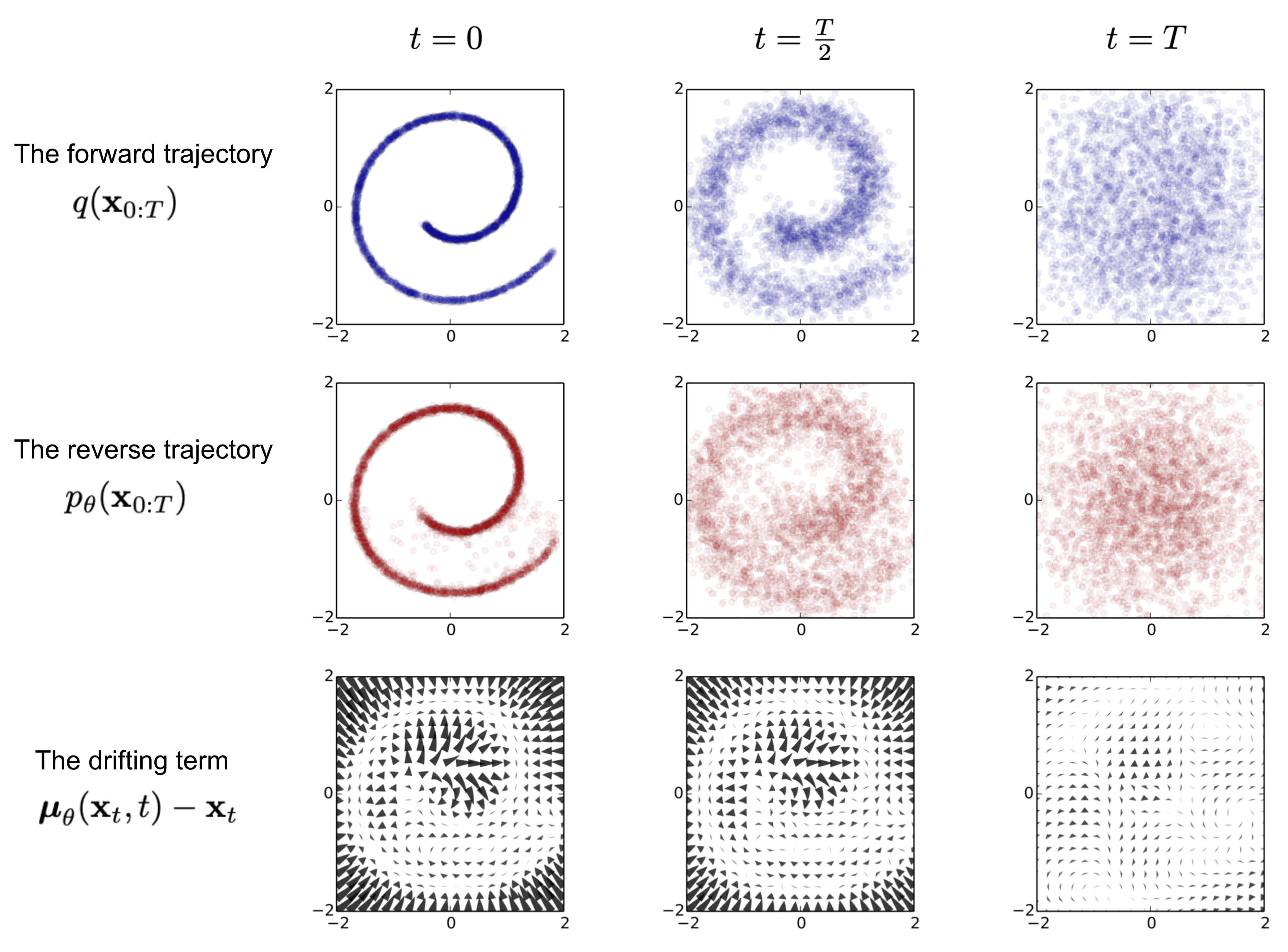
Fig. An example of training a diffusion model for modeling a 2D swiss roll data. [2]
实现这一目标的第一步是估计去噪步骤的均值和协方差(mean and covariance):
\[p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\mathcal{N}(\mu_{\theta}(\mathbf{x}_{t}, t), \Sigma_{\theta}(\mathbf{x}_{t}, t) ).\]在实践中,
- 可以通过神经网络估计 \(\mu_{\theta}(\mathbf{x}_{t}, t)\),
- \(\Sigma_{\theta}(\mathbf{x}_{t}, t)\) 可以固定为与 noising schedule 相关的常数,例如 \(\beta_{t}\mathbf{I}\)。
用这种方式估计 \(\mu_{\theta}(\mathbf{x}_{t}, t)\) 是可行的,但 Ho 等 [3] 提出了另一种训练方法: 训练一个神经网络 \(\epsilon_{\theta}(\mathbf{x}_{t}, t)\) 来预测前面公式 \(q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)\) 中的噪声 \(\epsilon\)。
与 Ho 等的方法类似[3],训练过程包括以下步骤:
- 采样图像 \(\mathbf{x}_{0}\sim q(\bf{x}_{0})\),
- 在扩散过程中选择特定的步骤 \(t \sim U(\{1,2,...,T\})\),
- 添加噪声 \(\epsilon \sim \mathcal{N}(0,\mathbf{I})\),
- 估计噪声 \(\epsilon_{\theta}(\mathbf{x}_{t}, t)= \epsilon_{\theta}(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \cdot \epsilon, t)\),
- 通过梯度下降学习网络上的损失 \(\nabla_{\theta} \|\epsilon - \epsilon_{\theta}(\mathbf{x}_{t}, t)\|^{2}\)。
一般来说,损失可以表示为
\[L_{\text{diffusion}}=\mathbb{E}_{t, \mathbf{x}_{0}, \epsilon}\left[\left\|\epsilon-\epsilon_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right],\]这里的公式、参数化和推导都没有详细展开,想深入了解推导过程,强烈推荐 [13-15]。
以上已经解释了为什么扩散模型也是一种生成模型。 一旦模型 \(\epsilon_{\theta}(\mathbf{x}_{t}, t)\) 训练好,就可以用它从加躁的 \(\mathbf{x}_{t}\) 回溯到原始图像 \(\mathbf{x}_{0}\)。 由于从各向同性高斯分布中采样噪声非常简单,我们可以获得无限的图像变化。
2.4 引导扩散(guiding the diffusion)
如果在训练过程中向神经网络提供额外的信息,就可以引导图像的生成。 假设图像已经打标(labeled),关于图像的类别信息 \(y\) 就可以送到 class-conditional diffusion model \(\epsilon_{\theta}(\mathbf{x}_{t}, t \mid y)\) 中。
-
引入指导的一种方式是训练一个单独的模型,该模型作为噪声图像的分类器(classifier of noisy images)。
在每个去噪步骤中,分类器检查图像是否以正确的方向去噪,并将自己的损失函数梯度计入扩散模型的整体损失中。
-
Ho & Salimans 提出了一种无需训练额外分类器,就能将类别信息输入模型的方法 [5]。
训练过程中,模型 \(\epsilon_{\theta}(\mathbf{x}_{t}, t \mid y)\) 有时(以固定概率)类别标签被替换为空标签 \(\emptyset\),也就是不显示实际的类别 \(y\)。 因此,它学会了在有和没有引导的情况下进行扩散。
对于推理,模型进行两次预测,一次给定类别标签 \(\epsilon_{\theta}(\mathbf{x}_{t}, t \mid y)\),一次不给定 \(\epsilon_{\theta}(\mathbf{x}_{t}, t \mid \emptyset)\)。 模型的最终预测变成乘以引导比例(guidance scale) \(s \geqslant 1\),
\[\hat{\epsilon}_{\theta}\left(\mathbf{x}_{t}, t \mid y\right)=\epsilon_{\theta}\left(\mathbf{x}_{t}, t \mid \emptyset\right)+s \cdot\left(\epsilon_{\theta}\left(\mathbf{x}_{t}, t \mid y\right)-\epsilon_{\theta}\left(\mathbf{x}_{t}, t \mid \emptyset\right)\right)\]这种无分类器引导(classifier-free guidance)复用主模型的理解力,不需要额外的分类器,Nichol 等的研究显示这种方式效果更好 [6]。
3 GLIDE:文本引导,定向扩散,2022.04
以上介绍了扩散模型的工作原理,现在要回答的两个问题是:
- 如何使用文本信息(textual information)来引导扩散模型?
- 如何确保模型的质量足够好?
GLIDE 论文见提出了非常新颖和有趣的见解 [6]。
3.1 架构
三个主要组件:
- 一个基于
UNet的模型:负责扩散的视觉部分(visual part of the diffusion learning), - 一个基于
Transformer的模型:负责将文本片段转换成文本嵌入(creating a text embedding from a snippet of text), - 一个
upsampling扩散模型:增大输出图像的分辨率。
前两个组件生成一个文本引导的图像,最后一个组件用于扩大图像并保持质量。
3.2 工作原理
GLIDE 模型的核心是著名的 UNet 架构 [8],用于扩散。
- 串联几个下采样和上采样卷积的残差层。
- 还包括 attention 层,这对于同时进行文本处理至关重要。
- 模型有约
2.3b个参数,并在与 DALL·E 相同的数据集上进行了训练。
用于引导的文本(text used for guidance)编码为 token,并送入 transformer 模型。
GLIDE 中使用的 transformer 有约 1.2b 个参数,
由 24 个 2048-width 的残差块构建。transformer 的输出有两个目的:
- 最终 embedding token 用作 \(\epsilon_{\theta}(\mathbf{x}_{t}, t \mid y)\) 中的 class embedding \(y\),
- final layer of token embeddings 添加到模型的每个 attention layer 中。
很明显,为了生成图像的准确性,大量精力放在了确保模型获得足够的与文本相关的上下文(text-related context)。 根据 text snippet embedding,模型将编码的文本与 attention 上下文拼接(concatenate),并在训练期间使用无分类器引导。
最后,使用扩散模型,通过一个 ImageNet upsampler
将图像从低分辨率转成高分辨率。
3.3 小结

Fig. GLIDE 效果。提示词 "a corgi in a field"(田野里一只柯基) [6]
GLIDE 融合了近年的几项技术精华,为文本引导图像生成带来了新的启示。 考虑到 DALL·E 模型是基于不同结构(非扩散)构建的,因此,可以说 GLIDE 开启了扩散式文生图时代。
4 DALL·E 2:取长补短,先验称奇,2022.04
OpenAI 团队马不停蹄,在 2022 年 4 月份以 DALL·E 2 [7] 再次震撼了整个互联网。 它组合了前面介绍的 CLIP 模型和 GLIDE 架构的精华。
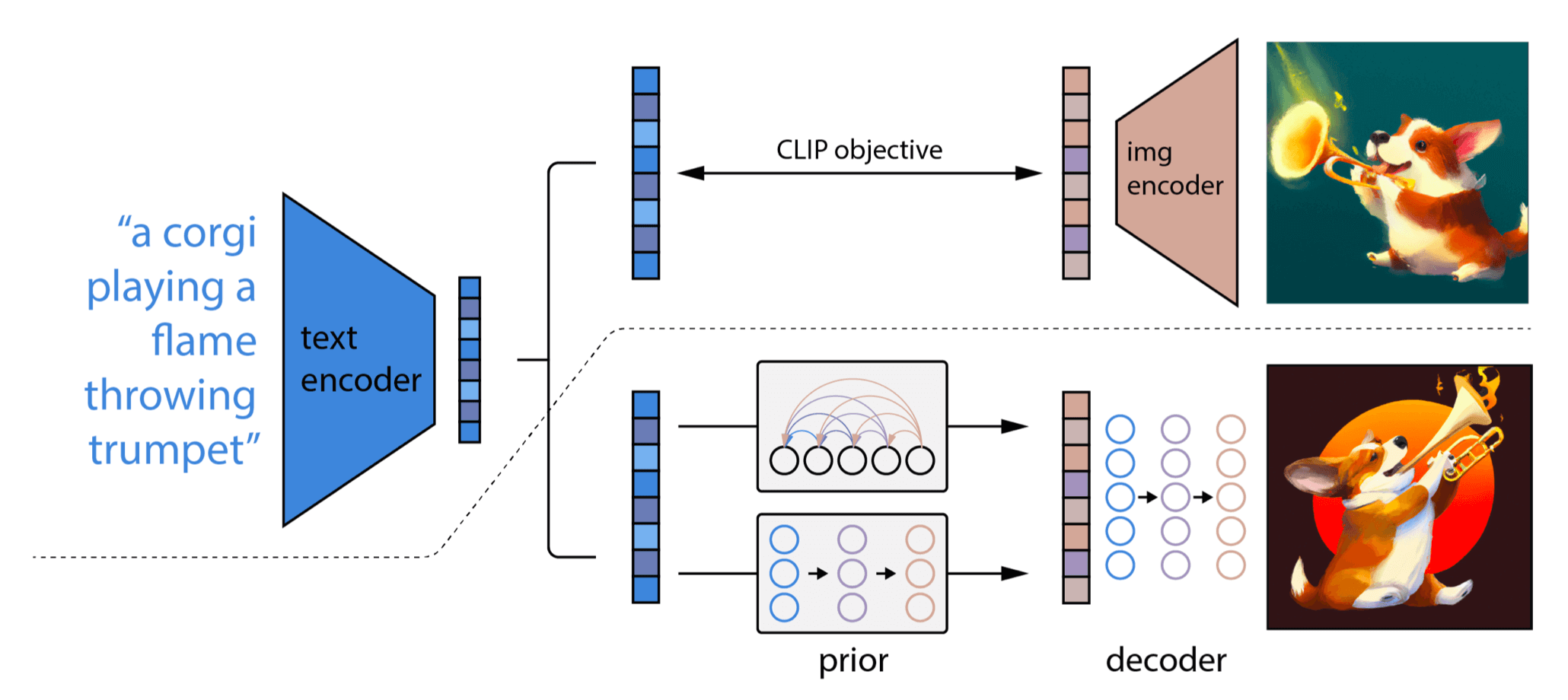
Fig. Visualization of DALL·E 2 two-stage mechanism. [13]
4.1 架构:unCLIP = prior + decoder
两个主要基础组件(也是两个阶段),
- prior
- decoder
二者组合产生图像输出。整个机制名为 unCLIP,
如果还记得前面介绍的 CLIP 机制,就能从 unCLIP 这个名字猜到底层可能是如何工作的。
4.2 The prior
第一阶段称为 prior,作用是将标题 —— 例如 “a corgi playing a flame throwing trumpet” ——
从文本转换成文本嵌入(text embedding)。
这个通过一个冻结参数的 CLIP 模型实现的。
4.2.1 为什么需要 prior 层(为什么单单 CLIP 不够)
前面介绍过,CLIP 模型记录的 text embedding 和 image embedding 的联合分布。所以, 直觉上来说,有了一个经过良好训练的 CLIP 模型,只要经过下面简单三步就能完成文生图的任务:
- 将文本(提示词)转换成对应的 text embedding;
- 将 text embedding 输入 CLIP 模型,获取最佳的 image embedding;
- 用 image embedding 通过扩散生成图像。
这里有问题吗?有,在第 2 步。DALL·E 2 的作者给了一个很好的解释:
“(在 CLIP 空间里)可能有无数的图像与给定的标题一致,因此两个编码器的输出不会完全一致。 因此,需要一个单独的 prior 模型来将 text embedding “翻译”为对应的 image embedding ”。
下面是对比:

Fig. 分别通过三种方式生成的图片:仅标题(caption)、标题+CLIP 和 prior-based。[7]
4.2.2 prior 选型:decoder-only transformer
作者对 prior 模型测试了两类模型:
- 自回归模型(autoregressive model)
- 扩散模型(diffusion model)
本文只讨论第二种:扩散 prior 模型。因为从计算角度来看,它的性能优于自回归模型。
为了训练 prior 模型,选择一个 decoder-only Transformer,
通过以下几个输入进行训练:
- 已编码的文本(encoded text)
- CLIP text embedding
- embedding for the diffusion timestep
- 加噪的 image embedding
目标是输出一个无噪的 image embedding (unnoised image embedding)\(z_{i}\)。
4.2.3 损失函数
直接预测未加噪声的 image embedding 而不是预测噪声更合适,这与之前讨论的 Ho 等提出的训练方式不同。 因此,回顾前面引导模型中扩散损失的公式
\[L_{\text{diffusion}}=\mathbb{E}_{t, \mathbf{x}_{0}, \epsilon}\left[\left\|\epsilon-\epsilon_{\theta}\left(\mathbf{x}_{t}, t\mid y\right)\right\|^{2}\right],\]我们可以将 prior 扩散损失(the prior diffusion loss)表示为
\[L_{\text{prior:diffusion}}=\mathbb{E}_{t}\left[\left\|z_{i}-f_{\theta}\left({z}_{i}^{t}, t \mid y\right)\right\|^{2}\right],\]其中
- \(f_{\theta}\):prior 模型
- \({z}_{i}^{t}\):带噪图像的嵌入
- \(t\):时间戳
- \(y\):用于引导的标题。
4.2.4 小结
以上就是 unCLIP 的前半部分,旨在生成一个能够将文本中的所有重要信息封装到 CLIP 样式的 image embedding 中的模型。
有了这个模型之后,就能根据用户输入的文本得到一个 image embedding。
而有了 image embedding,就能基于扩散模型反向(un-)生成最终的视觉输出 ——
这就是 unCLIP 名称的由来 —— 从 image embedding 回溯到图像,与训练 CLIP image encoder 的过程相反。
接下来看 DALL·E 2 中是如何实现这个反向过程的。
4.2 The decoder:基于 GLIDE 的改进
一个扩散模型的尽头是另一个扩散模型!(After one diffusion model it is time for another diffusion model!)。
在 DALL·E 2 中,“另一个扩散模型”就是前面已经介绍过的 GLIDE。
对 GLIDE 做了点修改,将 prior 输出的 CLIP image embedding 添加到 vanilla GLIDE text encoder 中。 其实这正是 prior 的训练目标 - 为 decoder 提供信息。
4.3 引导扩散和上采样
引导方式与普通的 GLIDE 一样。为改进效果,10% 概率将 CLIP embedding 设置为 \(\emptyset\),50% 概率设置文本标题 \(y\)。
跟 GLIDE 一样,在图像生成之后,利用另一个扩散模型进行上采样。 这次用了两个上采样模型(而不是原始 GLIDE 中的一个),一个将图像从 64x64 增加到 256x256,另一个进一步提高分辨率到 1024x1024。
5 Google Imagen:删繁就简,扩散三连,2022.05
DALL·E 2 发布不到两个月, Google Brain 团队也展示了自己的最新成果 - Imagen(Saharia 等 [7])。
5.1 架构:T5-XXL + Diffusion + Diffusion + Diffusion
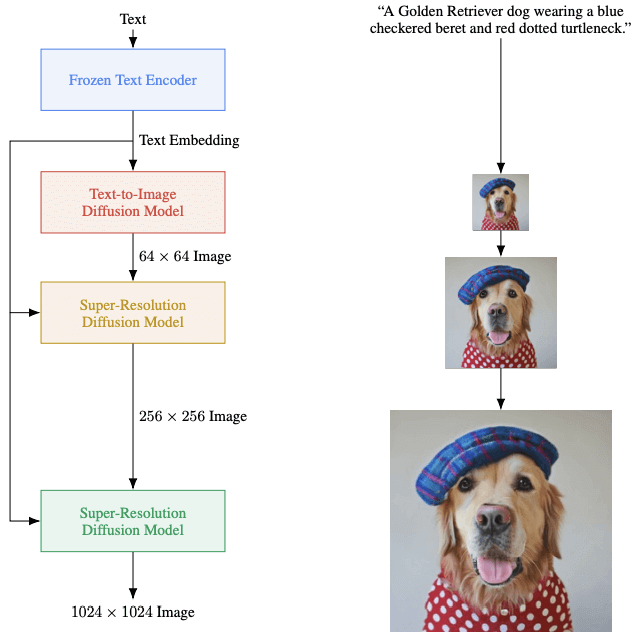
Fig. Overview of Imagen architecture. [7]
Imagen 架构在结构上非常简单:
- 预训练的文本模型用于创建 embedding,然后用这些 embedding 扩散成图像;
- 通过超分辨率扩散模型增加分辨率。
但架构中还是有一些新颖之处,比如模型本身和训练过程,总体来说还是先进一些。 这里只介绍下它与前面几个模型不同之处。
5.2 与 GLIDE、DALL·E 2 等架构的不同
5.2.1 使用预训练的 transformer (T5-XXL) 而不是从头开始训练
与 OpenAI 的工作相比,这是核心区别。
对于 text embedding,
- GLIDE 使用了一个新的、经过专门训练的 transformer 模型;
- Imagen 使用了一个预训练的、冻结的 T5-XXL 模型 [4]。
这里的想法是,T5-XXL 模型在语言处理方面比仅在图像标题上训练的模型有更多的上下文, 因此能够在不需要额外微调的情况下产生更有价值的 embedding。
5.2.2 使用更高效的底层神经网络(efficient U-net)
使用了称为 Efficient U-net 的升级版神经网络,
作为超分辨率扩散模型的核心。
比之前的版本更节省内存,更简单,并且收敛速度更快。 主要来自残差块和网络内部值的额外缩放。细节详见 [7]。
5.2.3 使用 conditioning augmentation 来增强图像保真度(image fidelity)
Imagen 可以视为是一系列扩散模型,因此在模型连接处 (areas where the models are linked)可以进行增强。
- Ho 等提出了一种称为条件增强(conditioning augmentation)的解决方案[10]。 简单来说就是在将低分辨率图像输入超分辨率模型之前对其 apply 多个 data augmentation 技术,如高斯模糊。
- 还有一些对于低 FID score 和高图像保真度至关重要的资源(例如 dynamic thresholding), 论文 [7] 中有详细解释。但这些方法的核心已经在前几节都涵盖了。
5.3 小结
截至 2022.04,Google’s Imagen 是最好的 text-to-image generation 模型。

Fig. Imagen 根据提示词生成的一些图片。[7]
6 总结
6.1 如何评估模型好坏
Imagen 的作者提供了两种评估方式,详见论文 [7]。
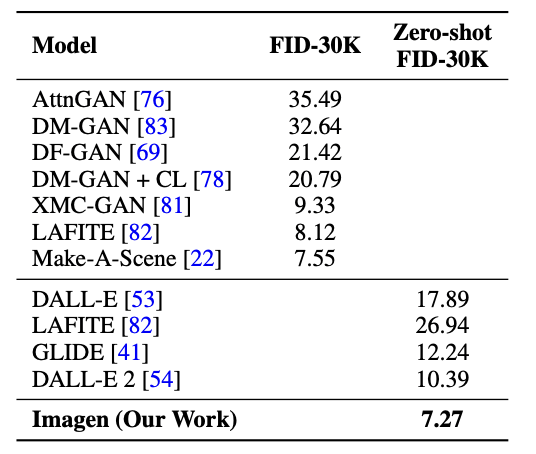
Fig. Comparison of several models. [7]
6.2 好玩儿的才刚开始
除了图像生成能力,文生图模型还有许多有趣的特征,比如图像修复、风格转换和图像编辑等等。
另一方面,扩散模型也还存在一些缺点,例如与以前的模型相比,采样速度较慢[16]。
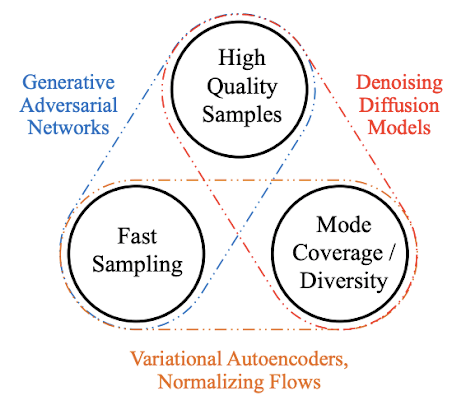
不同类型的文生图模型的考虑因素/优缺点 [16]
最后,对于喜欢深入实现细节的人,强烈推荐 [19],这是一些 github 项目, 众人手撸实现那些没有公开代码的模型。
参考资料
- Language Models are Few-Shot Learners Tom B. Brown et al. 2020
- Deep Unsupervised Learning using Nonequilibrium Thermodynamics 扩散数学原理,2015
- Denoising Diffusion Probabilistic Models 去噪扩散模型论文,基于 2,同一作者,2020
- How Much Knowledge Can You Pack Into the Parameters of a Language Model? Adam Roberts, Colin Raffel, Noam Shazeer. 2020
- Classifier-Free Diffusion Guidance Jonathan Ho, Tim Salimans. 2021
- GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models Alex Nichol et al. 2021
- Zero-Shot Text-to-Image Generation Aditya Ramesh et al. 2021
- Diffusion Models Beat GANs on Image Synthesis Prafulla Dhariwal, Alex Nichol. 2021
- Learning Transferable Visual Models From Natural Language Supervision Alec Radford et al. 2021
- Cascaded Diffusion Models for High Fidelity Image Generation Jonathan Ho et al. 2021
- Hierarchical Text-Conditional Image Generation with CLIP Latents Aditya Ramesh et al. 2022
- Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding Chitwan Saharia et al. 2022
- What are Diffusion Models? 数学推导,Lilian Weng. 2021
- Diffusion Models as a kind of VAE 数学推导,Angus Turner. 2021
- An introduction to Diffusion Probabilistic Models 数学推导,Ayan Das. 2021
- Improving Diffusion Models as an Alternative To GANs, Part 1 Arash Vahdat, Karsten Kreis. 2022
- DrawBench prompts Google Brain team. 2022
- DALL·E 2 subreddit Reddit. 2022
- Phil Wang’s repositories Phil Wang. 2022

